Excel Homework Help – Excel Assignment Solutions for Students

So you have a Microsoft Excel assignment and... it seems that you are not going to complete it in time, on your own. We are here to help with Excel assignments - by providing solutions instead of tutoring. Nevertheless, let us know if you have any questions about the solution and we will be happy to explain it.

Students face various roadblocks: not sure where to start, difficult functions, ambiguous questions, Excel on Mac doesn’t load, expensive licenses, etc. It doesn't matter - simply provide us with the necessary materials and relax.

Operating since 2013, we have accumulated experience to help with any Excel project, no matter if it is a beginner or advanced level. It is now easier than ever to overcome your struggles by using an online Excel assignment help service.

What Students Are Being Taught Excel?

It is not just you - everybody from Physics students to Management students is introduced to MS Excel. Why so? It is an essential tool in data storage and quick yet powerful analysis, while also being intuitive. Excel offers the functionality of a regular programming language while letting users achieve it mainly by mouse-clicking on the graphic interface, without obtaining specialized programming knowledge. Subjects like economics, finance, and business analysis are hardly imagined without using Excel in one way or the other. Most tasks solved in Excel are of a general kind – they are subject-independent. This is why we can offer homework help with Excel in a wide variety of disciplines.

Excel was the first mover in the field of data spreadsheets and it is still the keystone product of Microsoft. However, lately, some alternatives have emerged such as Tableau or Google sheets that take up a portion of the market. But you can be certain - Excel is here to stay. Your knowledge would not become obsolete, so it is worth putting the effort into studies.

It is often the case that data analysis using Excel is just an intermediate step of some bigger decision process. After the Excel part of the work is complete, one might need to write a report describing the key findings (in Word or PDF document). Alternatively, a slide presentation is prepared (usually using PowerPoint) to present the findings among interested parties, very often in front of the class.

Popular Excel Assignments That We Often Help With

1. VLOOKUP. This might look strange, but many students cannot use VLOOKUP in their homework properly. We can teach you the correct way of choosing the function parameters. Related to this are INDEX and MATCH functions. The combo of these two is equivalent to VLOOKUP (or HLOOKUP).
2. Finance and Economics. It is a broad topic, ranging from stock returns calculation to Pareto front calculations. Data table entry and conditional calculations (using IF, AND, OR) are typical for these kinds of homework.
3. Mortgage calculation, Loan amortization table. Formulas in use: PMT, IPMT, PPMT, CPMT, etc. The calculation result is displayed as a payment value for monthly payments together with a breakdown of payment parts. Alternatively, you could be asked to calculate some value (e.g. cumulative interest paid over loan lifetime) while having other variables fixed.
4. Linear Regression. It is usually the first approach method in data modeling. A data analysis toolbox is used for this calculation. Unfortunately, Excel practitioners are not well-versed in statistics and rarely check for linear regression model assumptions. Ignoring this crucial part can lead to the resulting model looking nice while being totally wrong.
5. Data Entry Validation and Conditional Formatting. These are very useful tools to assist in outlier detection, but regular Excel user never uses them. This is why students might need help with such assignment solutions.
6. What-If analysis: Goal-seek, Scenario manager, and Data tables. These are intermediate-difficulty assignments. It is not plain simple on how to achieve the assignment instruction requirements while dealing with this analysis.

Automated Excel Class: Pearson CIS, MyITLab, SIMnet, SAM

Automated grading of Excel assignments has recently gotten extremely popular. Such tasks ask you to follow the instructions from Word Instructions Document to edit the Excel spreadsheet. This kind of assignment doesn’t test your ability to think creatively or solve ill-defined problems. They are used for a mechanic evaluation of technical Excel skills and must be completed in exactly the way you are taught in class. In fact, you are "punished" for being creative – automatic graders might not understand your formula even if it is correct, but written in some other way than expected. This is why students get desperate and ask for our assistance.

We help with unique solutions to Pearson CIS, MyITLab, SIMnet, or SAM project assignments. You never get caught for plagiarism and receive top marks: Capstone Project, CapAssesment, and final exams.

One extra reason for using our services for automated graders is that Excel software is too expensive to buy for a single class. You have extra problems if you are a Mac user – it simply does not work on Mac! So you might need to get another computer to complete your homework to pass the class. It is way cheaper to use our Excel help.

Popular More Advanced Excel Assignments

Advanced Excel problems cannot be graded automatically because they are open-ended, the solution depends on chosen perspective and subjective evaluation of assumptions and the data. The situation is similar to essay writing in top universities versus fixed technical tasks in "cheaper" universities – extra resources are necessary to prepare and grade the open-ended questions.

1. Pivot Tables and Pivot Charts. These are very powerful tools of Excel – Pivot table has many functions similar to a proper relational database system like SQL. Flexible user-oriented filtering, data aggregation, and segregation methods are what you really need to extract knowledge from your data. Pivot Charts work hand-in-hand with Pivot tables, offering dynamic visualization of your data. Results are very attractive as the Pivot chart example shown below:

   

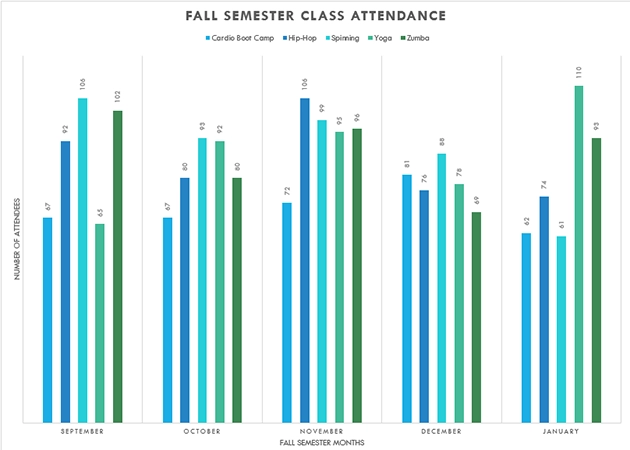
2. VBA. Visual Basic is an old and "ugly" programming language. However, it is highly functional and works perfectly for Excel Object manipulation. Using VBA you can automate mechanical tasks that you would otherwise do by hand. By using Excel you don’t need to program as in a regular programming language. The formulas of Excel are often the first step towards programming, while VBA is considered a programming-based solution to Excel problems. It has all essential programming functionality, like looping through Excel cells, conditional logic of comparing values, and setting variables.
3. Excel Macros is a nice functionality in-between graphical user interface in Excel and VBA code. It records your actions and translates them into VBA program code. However, lots of unnecessary code gets generated and you need to understand how to edit your recorded code properly. Macro recording gets you a jumpstart in writing a VBA automation script – instead of looking for explanations in the online documentation, students can generate partial solutions without any programming knowledge. Both macros and VBA are "hidden" from a regular user under the Developer tab (you must enable it in Excel options).
4. ActiveX Controls: Button, Combo Box, Etc. This extra visual "web-like" functionality is reachable from developer mode. All the buttons and forms work as VBA commands, so if you want to use these functions you better be ready for some VBA programming.
5. Other: Probabilities-Related Tasks. These cover a wide range of statistical calculations, like sampling from distributions or probability evaluations of some range in data. Our advice is to use "real programming languages" for such goals, like R or Python. Nevertheless, we can help with advanced calculations.

Excel Solver Help for Linear Optimization Assignments

We consider optimization assignments as a difficult, but separate class from the others. In mathematics, it is called operations research. So you might be asked to deliver not only an Excel Solver solution but also a mathematical justification for it. To get started using solver you need to turn on the optimization add-in. It is not a basic functionality of Excel, because deep knowledge is often required to achieve the results.

How Does Solver Optimization Homework Look Like?

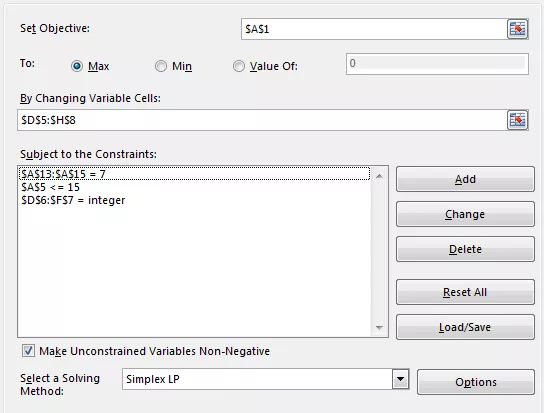
Explaining the full example task is simply not feasible in this article. Excel solver restrictions entry interface requires you to:

• Set objective. Choose a single cell to be minimized, optimized, or become an exact value.
• Set variable cells – one or more cells to variate
• Add single or multiple constraints (equal, more, less, binary, etc.)
• Select a Solving Method. Simplex LP is a linear programming method. For it to work, all the constraints must be linearly dependent. The solution is guaranteed in such a case. If you have non-linear restrictions (like some Excel function or multiplication of variables) you must use other methods, but they are not guaranteed to find a unique solution.

When to Consider Receiving Excel Homework Help?

There are various reasons why students need to buy Excel homework help, some of them already mentioned in the article. You can think of such help as tutoring or as outsourcing the hard work when the outcome is worth it. Your position depends on the situation you find yourself in. Sometimes there is no time for studies and you are pressured to deliver, other times your computer just got broken. The cause really does not matter – the value of the exchange is what matters.

Over the years, our online Excel helpers have completed thousands of homeworks. It is very likely that you will find yourself staring at Excel sheets later in your career. Then you will have real problems to solve and you will know exactly what you need to do, instead of solving various "fake" assignments in college or university. Our clients graduate with the best grades leading to top positions in the business world. We wish you the best.

Regards, HomeworkHelpOnline.net Team